Метою лабораторної роботи є вивчення дискретного перетворення Фур’є (ДПФ) з реалізацією фільтра FIR з використанням швидкого перетворення Фур'є для згортки.
Вступ
Дискретне перетворення Фур'є - це один з найважливіших інструментів цифрової обробки сигналів. Є три найбільш поширених варіанти використання ДПФ. Перший з них - це обчислення частотного спектра сигналу. Обчислення спектру безпосередньо дозволяє розкрити інформацію, закладену в частоті, фазі і амплітуді гармонійних компонентів, на які розкладається сигнал. Прикладом такого представлення інформації і системи, що її розпізнає, можуть служити мова і слух людини. Другий варіант використання ДПФ пов'язаний з розрахунком частотної характеристики системи по її імпульсній характеристиці або навпаки. Перехід до частотної характеристики дозволяє вести аналіз і опис систем в частотній області, що є альтернативою опису в часовій області і застосування згортки. А третій варіант використовує ДПФ як проміжний етап більш складних перетворень сигналу. Класичним прикладом цього є реалізація згортки в частотній області - швидка згортка, на виконання якої витрачається в сотні разів менше часу, ніж на традиційну.
Дискретне перетворення Фур'є (ДПФ) є перетворенням Фур'є, яке може бути обчислено на цифровому комп'ютері. Реалізація ДПФ вимагає багато комплексних множень і додавань. Кількість комплексних множень і додавань може бути значно зменшена за рахунок ефективного рекурсивного N-точкового ДПФ, коли N є степінь 2. Ці алгоритми ДПФ відомі як алгоритми швидкого перетворення Фур'є (FFT) (існує кілька ефективних кодів, які були майже еквівалентні FFT). Алгоритм ШПФ був представлений для обробки сигналів в 1965 році в статті авторів Кулі і Тьюкі (Cooley–Tukey). Однак сама ідея виникла більш ніж за сто років до цього у німецького математика К.Ф. Гауса в 1805 році. Але його роботи з даної теми виявилися забутими через відсутність цифрових комп'ютерів, в яких цей підхід можна було б застосувати на практиці.
Пряме комплексне ШПФ при використанні полярної форми запису виражається наступним співвідношенням:
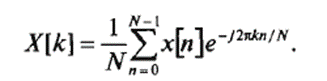
Використовуючи формулу Ейлера, можна перейти до алгебраїчної формі записи прямого ДПФ:
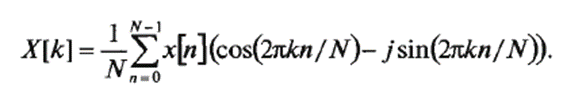
В комплексному ШПФ масиви х[п] і Х[к] є комплексними. Зверніть увагу на те, що ми можемо не використовувати уявну частину масивів в часовій області. Припустимо, потрібно обробити дійсний сигнал - послідовність відліків напруги, отриманих в дискретні моменти часу. Ці значення присвоюється дійсній частині, а уявній частині відліків присвоюється нульові значення.
Формула зворотного комплексного ДПФ має наступний вигляд:
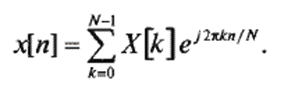
Примітка. Загальне поняття перетворення Фур'є охоплює 4 класи перетворень, що виділяються відповідно до типів сигналів (неперервні і дискретні, періодичні і аперіодичні), якими вони оперують:

Швидкість оновлення спектру сигналу
Припустимо, що ми графічно хочемо відобразити спектр сигналу на основі FFT. Для FFT потрібний кадр (блок) даних. Якщо припустимо, що частота дискретизації Fs = 48 кГц (період вибірки Ts = 1 / 48000 = 20.83 мкс ) і розмір кадру 2048 вибірок, то спектр може не бути оновлений не швидше, ніж кожних 2048 * 20.83 мкс = 42.66 мс, що еквівалентно 23,44 оновлень дисплею в секунду. За телевізійним стандартом зображення оновлюються 25 або 30 кадрів в секунду, а фільми в кінотеатрах зазвичай оновлюються з частотою 24 кадри в секунду, так що 23,44 оновлень може бути задовільним. Зверніть увагу на те, що в цьому прикладі ми тепер маємо 42.66 мс або більше 42660000 тактових циклів процесора (для частоти 1ГГц) для обробки даних! Якщо ми подвоюємо розмір кадру, то отримаємо в два рази більше часу для обробки даних, однак частота оновлення спектру зменшиться вдвічі, що не може бути прийнятними для користувача.
Розмір кадру є одним з багатьох нюансів інженерного проектування, який має бути врахований при проектуванні системи. Якщо вихідні блоки посилаються на ЦАП, то вони будуть перетворені в аналоговий сигнал вибірка за вибіркою на заданій частоті вибірки Fs. Для правильної роботи наступний блок сигналу для виведення повинен бути готовий на той час, коли перетвориться остання вибірка поточного блоку. Наприклад, якщо ми виконуємо обробку звуку, це гарантує, що з точки зору слухача не буде ніякого «розриву» в музиці, і на виході вона не буде звучати інакше, ніж при використанні безблокової обробки. Звичайно, є часовий лаг або затримка, яка рівна періоду блоку, але вона непомітна для слухача.
Більшість DSP режиму реального часу, таких як CD і DVD-плеєри, системи телефонного зв'язку (наземні лінії і бездротовий стільниковий зв'язок), інтернет-комунікації і цифрове телебачення (таких як HDTV) реалізовані на основі блокової (кадрової) обробки сигналів. Наприклад, програвачі компакт-дисків використовують кадр даних, який складається з шести періодів вибірки (шість вибірок лівого каналу, шість вибірок правого каналу, чергуючись). Кожна вибірка займає два байти (16-біт), тому початковий розмір кадру становить 24 байт. Додаткові кроки обробки, в тому числі, виправлення помилок і модуляція, розширюють розмір кадру до 73,5 байт (588 біт), що насправді зберігається на компакт-диску.
Зверніть увагу, що для процесу в режимі реального часу, збір вибірок за допомогою АЦП ніколи не зупиняється доти, поки система знаходиться в робочому стані. Коли отримані N вибірок, вони передаються для обробки за допомогою DMA і збір нового блоку даних виконується безперервно.
Обчислення швидкого перетворення Фур’є
Для обчислення ШПФ у бібліотеці функцій цифрової обробки сигналів (ЦОС) під цифровий сигнальний процесор С6678 є ряд функцій, прототипи яких наведені в заголовному файлі dsplib.h. Ці функції працюють з цілочисельними (функції з DSP в назві) та дійсними (функції з DSPF_ в назві) типами даних. Серед функцій, які працюють з дійсними типами даних є DSPF_dp_fftDPxDP та DSPF_sp_fftSPxSP, які працюють, відповідно, для даних подвійної точності (double) і одинарної точності (float). Для нашого прикладу скористаємося функцією ШПФ DSPF_sp_fftSPxSP з вхідними комплексними даними. Вона має наступний синтаксис:
void DSPF_sp_fftSPxSP( int N,
float *ptr_x,
float *ptr_w,
float *ptr_y,
unsigned char *brev,
int n_min,
int offset,
int n_max );
Перший аргумент функції N – розмір ШПФ. Значення N повинно бути ступенем 2 та 8 ≤ N ≤ 131072 точок. Бажано щоб 32 <= N.
Другий аргумент функції ptr_x - вказівник на масив комплексних вхідних даних
Третій аргумент функції ptr_w – вказівник на масив, що містить таблицю синусів і косинусів, яка необхідна для обчислення ШПФ.
Четвертий аргумент функції ptr_y - вказівник на масив комплексних вихідних даних
П’ятий аргумент функції brev - вказівник на зворотну бітову таблицю, яка містить 64 записи. Алгоритм метелика DSPF_sp_fftSPxSP є зворотним, що робить дані в зворотному бітовому вигляді. Тому використовується проста таблиця, щоб зробити розворот бітів. Ця таблиця має вигляд:
unsigned char brev[64] = {
0x0, 0x20, 0x10, 0x30, 0x8, 0x28, 0x18, 0x38,
0x4, 0x24, 0x14, 0x34, 0xc, 0x2c, 0x1c, 0x3c,
0x2, 0x22, 0x12, 0x32, 0xa, 0x2a, 0x1a, 0x3a,
0x6, 0x26, 0x16, 0x36, 0xe, 0x2e, 0x1e, 0x3e,
0x1, 0x21, 0x11, 0x31, 0x9, 0x29, 0x19, 0x39,
0x5, 0x25, 0x15, 0x35, 0xd, 0x2d, 0x1d, 0x3d,
0x3, 0x23, 0x13, 0x33, 0xb, 0x2b, 0x1b, 0x3b,
0x7, 0x27, 0x17, 0x37, 0xf, 0x2f, 0x1f, 0x3f
};
Шостий аргумент функції n_min - має бути 4, якщо N представляється як степінь 4, інакше, n_min повинно бути 2.
N може бути степінь 4 або 2. Якщо N є степінь 4, то radix = 4, а якщо N є 2, то radix = 2. «radix» використовуються для контролю на скільки етапів виконуються розкладання масиву. Він також використовується, щоб визначити, чи слід виконувати розкладання Radix-4 або Radix-2 на останній стадії.
Сьомий аргумент функції offset - індекс елемента для комплексних даних від початку основного масиву, щоб обчислити sub-fft. Часто дорівнює 0.
Восьмий аргумент функції n_max - розмір основного FFT для комплексних даних. Часто дорівнює N.
Комплексні дані ptr_x , ptr_y і масив синусів і косинусів ptr_w мають бути вирівняні по межах подвійного слова (8 байт). Дійсні значення зберігаються на парних позиціях слів (0, 2, 4…), а уявні значення на непарних позиціях (1, 3, 5…).
Для ініціалізації масиву ptr_w може бути використана функція tw_gen(w_sp, N).
Ще одна функція, яка буде потрібна для подання результатів у зручній формі - це функція обчислення модуля комплексного числа magnitude(…).
Функції далі приведені у коді програми.
Створення проекту в середовищі
1. Запустіть CCS.
2. Створіть проект за інструкціями лабораторної роботи 6 або використовуйте копію проекту лабораторної роботи 6.
3. У файл main.c вставити наступний код:
#include <stdlib.h>
#include <math.h>
#include <inc/dsplib.h>
/* Global definitions */
//#define _LITTLE_ENDIAN
/* Число вибірок для яких необхідно виконати ШПФ*/
#define N 512
unsigned char brev[64] = {
0x0, 0x20, 0x10, 0x30, 0x8, 0x28, 0x18, 0x38,
0x4, 0x24, 0x14, 0x34, 0xc, 0x2c, 0x1c, 0x3c,
0x2, 0x22, 0x12, 0x32, 0xa, 0x2a, 0x1a, 0x3a,
0x6, 0x26, 0x16, 0x36, 0xe, 0x2e, 0x1e, 0x3e,
0x1, 0x21, 0x11, 0x31, 0x9, 0x29, 0x19, 0x39,
0x5, 0x25, 0x15, 0x35, 0xd, 0x2d, 0x1d, 0x3d,
0x3, 0x23, 0x13, 0x33, 0xb, 0x2b, 0x1b, 0x3b,
0x7, 0x27, 0x17, 0x37, 0xf, 0x2f, 0x1f, 0x3f
};
/* вирівнювання даних має бути подвійне слово 8 */
#define AL 8
/* масив відліків вхідного сигналу та вихідного */
#pragma DATA_ALIGN(in_signal,AL) // вирівнювання
float in_signal [2*N]; // для заповнення сигналом
// 2*N - для REAL i IMAGIN складових комплексного сигналу
/* масив відліків вхідного сигналу та вихідного для ШПФ */
#pragma DATA_ALIGN(in_sig_fft,AL) // вирівнювання
float in_sig_fft [2*N]; // для заповнення сигналом
// після ШПФ цей масив зміниться
#pragma DATA_ALIGN(out_signal,AL) // вирівнювання
float out_signal [2*N]; // для спектру сигналу
#pragma DATA_ALIGN(w_sp, AL)
float w_sp [N]; // для таблиці cos | sin - Twiddle factor
// масиви для дійсної і уявної складових вихідного сигналу
float y_real_sp [N];
float y_imag_sp [N];
// масив для модуля дійсної і уявної складових
float a4h[N];
// прототипи ф-ій
void generateInput();
void seperateRealImg (float *real, float * img, float * cmplx, int size_cmplx);
void tw_gen (float *w, int n);
void magnitude(float *in_real, float * in_img, float * out_arr, int size);
int main(void) {
int i;
/* Генерування сигналу */
generateInput();
/* Функція генерує масив (таблицю) косинусів та сінусів*/
tw_gen(w_sp, N);
// реалізація ШПФ
DSPF_sp_fftSPxSP(N, in_sig_fft, w_sp, out_signal, brev, 4, 0, N);
/* розділення комплексного сигналу на real і imaginary дані */
seperateRealImg (y_real_sp, y_imag_sp, out_signal, N);
// модуль
magnitude (y_real_sp, y_imag_sp, a4h, N);
i=0;// breakpoint
return 0;
}
/*
Функція генерує сигнал певної частоти і записує відліки в масив
*/
void generateInput () {
int i;
float FreqSignal1, sinWaveMag1 ;
float FreqSignal2, sinWaveMag2 ;
float real_s, img_s ; // для реальної та уявної складової
float FreqSample;
/* частота дискретизації Hz*/
FreqSample = 48000;
/* Амплітуда сигналу */
sinWaveMag1 = 5;
sinWaveMag2 = 10;
/* частота сигналу Hz*/
FreqSignal1 = 2000;
FreqSignal2 = 5550;
/* генерування сигналу дійсних та уявних складових сигналу */
for (i = 0; i < N; i++) {
real_s = (float) (
sinWaveMag1 * cos(2*3.14*i * FreqSignal1 /FreqSample)+
sinWaveMag2 * cos(2*3.14*i* FreqSignal2 /FreqSample)
);
img_s = (float)0.0;
in_signal[2*i] = real_s;
in_signal[2*i + 1] = img_s;
}
// копія масиву в in_sig_fft
for (i = 0; i < N; i++) {
in_sig_fft[2*i] = in_signal[2*i];
in_sig_fft[2*i + 1] = in_signal[2*i+1];
}
}
/*
Функція генерує масив (таблицю) косинусів та сінусів для ШПФ
*/
void tw_gen (float *w, int n)
{
int i, j, k;
const double PI = 3.141592654;
for (j = 1, k = 0; j <= n >> 2; j = j << 2)
{
for (i = 0; i < n >> 2; i += j)
{
#ifdef _LITTLE_ENDIAN
w[k] = (float) sin (2 * PI * i / n);
w[k + 1] = (float) cos (2 * PI * i / n);
w[k + 2] = (float) sin (4 * PI * i / n);
w[k + 3] = (float) cos (4 * PI * i / n);
w[k + 4] = (float) sin (6 * PI * i / n);
w[k + 5] = (float) cos (6 * PI * i / n);
#else
w[k] = (float) cos (2 * PI * i / n);
w[k + 1] = (float) -sin (2 * PI * i / n);
w[k + 2] = (float) cos (4 * PI * i / n);
w[k + 3] = (float) -sin (4 * PI * i / n);
w[k + 4] = (float) cos (6 * PI * i / n);
w[k + 5] = (float) -sin (6 * PI * i / n);
#endif
k += 6;
}
}
}
/*
Функція seperateRealImg
для розділення real and imaginary даних після ШПФ
Вона потрібна для того, щоб відобразити графічно дані,
використовуючи CCS graph
*/
void seperateRealImg (float *real, float * img, float * cmplx, int size_cmplx) {
int i, j;
for (i = 0, j = 0; j < size_cmplx; i+=2, j++) {
real[j] = cmplx[i];
img[j] = cmplx[i + 1];
}
}
/*
Функція обчислення модуля комплексного числа
*/
void magnitude(float *in_real, float * in_img, float * out_arr, int size){
int i;
for (i = 0; i < size; i++) {
out_arr[i] = (float)sqrt(in_real[i]* in_real[i] + in_img[i]*in_img[i]);
}
}
4. Побудуйте проект та загрузіть програму в процесор.
5. Отримайте результати та порівняйте їх з результатами, що зображені нижче. Вони повинні співпадати.
Результати
Сигнал:
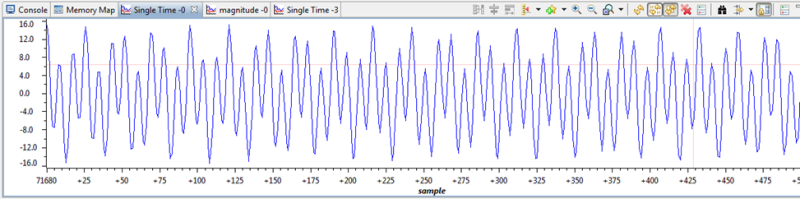
Спектр сигналу, побудований за допомогою Tools -> Graph -> FFT Magnitude:

На даному графіку зображено тільки частотний діапазон [0; Fd/2].
Спектр сигналу, отриманий за допомогою ф-ії DSPF_sp_fftSPxSP:
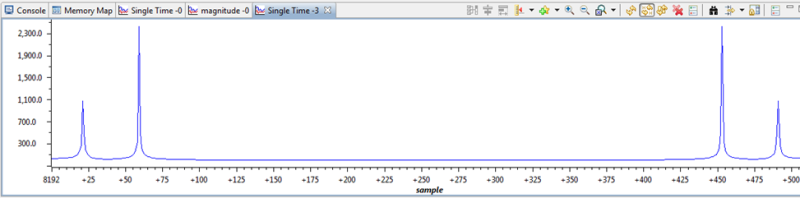
Як видно, результати дещо відрізняється від наших очікувань (очікуємо 2 гармоніки), також їх амплітуди не збігається з амплітудами сигналів, і вісь абсцис не відображає частоту (відображаюся номера елементів масиву з кроком 1).
Налаштування для трьох графіків:

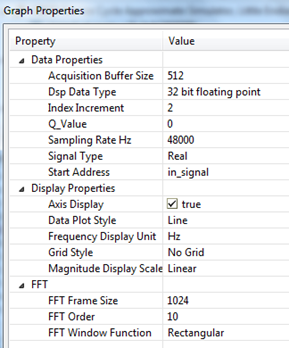
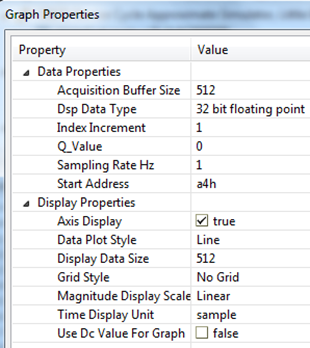
Необхідно враховувати, що алгоритм перебирає не тільки позитивні, але і негативні частоти, і права частина графіка є «дзеркальним» відображенням реального спектру. Якщо подивитися на фази частот, можна помітити, що вони рівні негативним фазам відповідним негативним частотам. Враховуючи рівність амплітуд лівої і правої частини спектру і відповідність їх фаз з точністю до знаку, весь спектр буде еквівалентний своїй позитивній частині з подвоєною амплітудою. Виняток становить тільки 0 елемент, який не має дзеркальної половини.
Оскільки ШПФ фактично являє собою підсумовування сигналу перемноженого на ядро перетворення (комплексну експоненту) для кожної з частот, то реальна амплітуда буде меншою у кількість підсумовувань N.
Таким чином, просто відкиньте кінець вихідного масиву і помножте елементи на 2 (за винятком постійної складової). Отримані значення елементів розділіть на кількість елементів N. Також розрахуйте з яким кроком слідують частоти в спектрі.
Отримайте наступний графік:
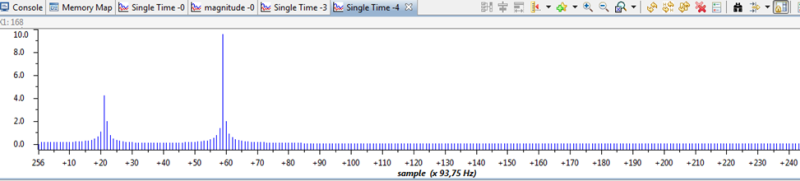
Бачимо реалізований на базі DSP аналізатор спектру сигналу.
Завдання
1. Згенерувати сигнал - «Сума 4 гармонік» та побудувати його спектр. Сума гармонійних коливань належить звуковому діапазону частот. Частота дискретизації 48 кГц. Частоти гармонік довільні.
2. Збільшити розмір ШПФ до 1024 доповнивши масив нулями. Спостерігати зміни. Розрахуйте з яким кроком слідують частоти в спектрі.
3. Згенерувати прямокутний імпульс тривалістю 50 вибірок. Записати значення вибірок в дійсну частину масиву. Виконати ШПФ та відобразити графіки уявної та дійсної частини вихідного сигналу. Зберегти до файлу для подальшого аналізу.
4. Аналогічно пункту 3 записати значення вибірок прямокутного сигналу в уявну частину масиву. Отримати графіки уявної та дійсної частини вихідного сигналу.
Домашнє завдання
Розробити СІХ (FIR) фільтр. Та реалізувати його за допомогою алгоритму швидкої згортки. Вибір фільтру та його характеристик довільний. Результати фільтрації представити на графіках.
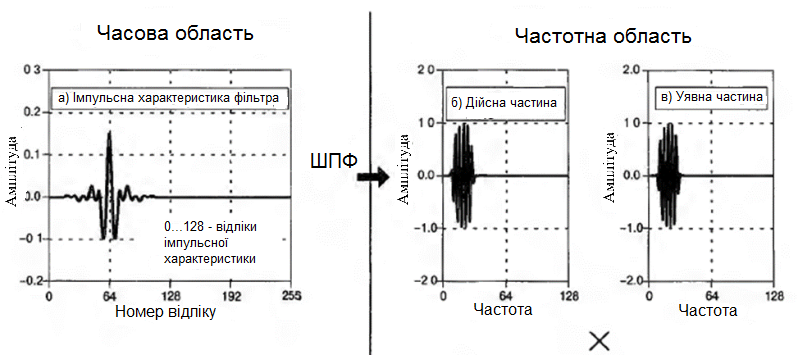
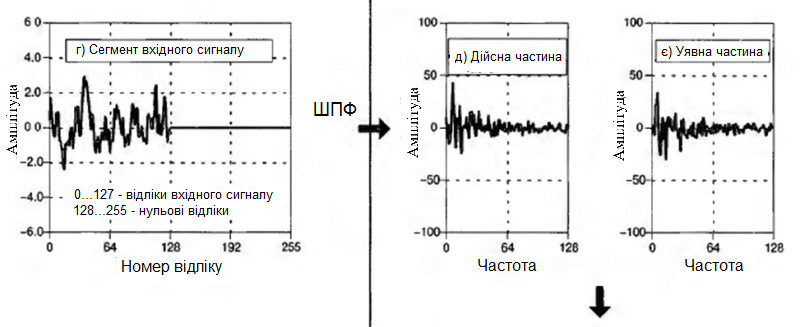
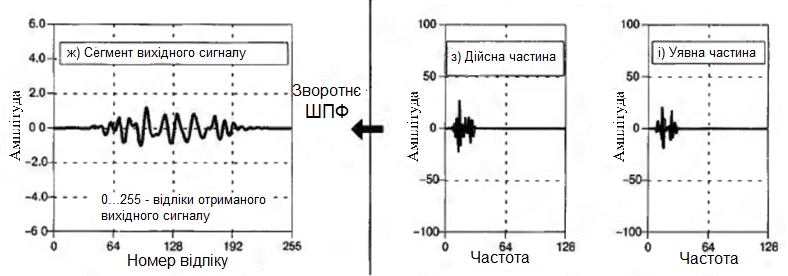
Алгоритм швидкої згортки дозволяє замінити операцію згортки множенням частотних спектрів відповідних сигналів. За допомогою ШПФ вхідний сигнал переводиться в частотну область, де він множиться на частотну характеристику фільтра, після чого знову переноситься в часову область за допомогою зворотного ШПФ.
Для фільтрів, порядок яких перевищує 64, перехід до швидкої згортку значно скорочує обсяг необхідних обчислювальних витрат, при цьому всі характеристики фільтрів залишаються незмінними.
Для реалізації алгоритму використовуйте функції : DSPF_sp_fftSPXSP, DSPF_sp_ifftSPxSP (зворотнє ШПФ), DSPF_sp_vecmul (поелементне множення масивів).
Порядок БПФ повинен бути обраний досить великим, щоб виключити можливий вплив циклічної згортки. Наприклад, порядок фільтра дорівнює 129, а вхідний сигнал - 128 відліків, тому довжина вихідного сегмента дорівнює (129+128-1=) 256 відліків. Отже, необхідно використовувати БПФ 256-го порядку.
Приклад реалізації наведений на рис. нижче:
Література
1. MATLAB и быстрое преобразование Фурье. https://habrahabr.ru/post/112068/
2. Простыми словами о преобразовании Фурье. https://habrahabr.ru/post/196374/
3. Смит, Стивен. Цифровая обработка сигналов. Практическое руководство для инженеров и
научных работников/ Стивен Смит; пер. с англ. А. Ю. Линовича, С. В. Витязева, И. С. Гусинского. - М.: Додэка-ХХI, 2012.



